2D data regression: Python Ordinary Kriging interpolation code

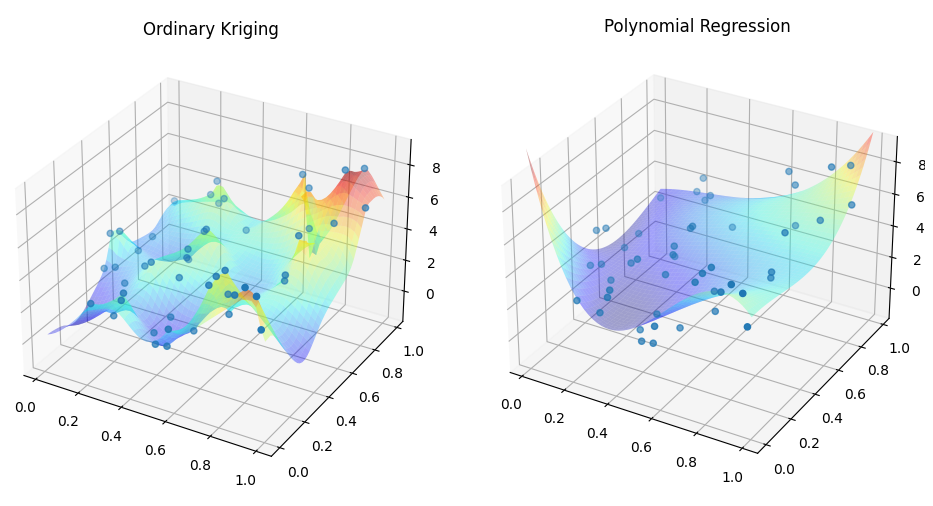
Ordinary Kriging is one of the technique to build data-exact, best linear unbiased estimator. Goal here is to write a code to perform ordinary kriging using 2-D simple dataset, then compare the results with simple 3rd order polynomial function.

First, results obtained below code are shown below.

import itertools
import os
import numpy as np
import matplotlib.cm as cm
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def main():
    pass



def Test_Okriging(x,y,Obsp,xx,yy,nget,sill,rnge):

    nobs = len(Obsp)

    A  = np.ones((nobs+1,nobs+1)) # = 1 for lagrange multiplier
    b  = np.ones((nobs+1,1))
    Cd = np.ones((nobs+1,nobs+1))

    b[nobs]= 1   # 1 = lagrange multiple

    pos = np.ones((nobs,2))
    pos[:,0] = x/np.max(x)
    pos[:,1] = y/np.max(y)

    # Variogram_Generation(Cd,A,Obsp,pos,nget,sill,rnge)
    #------------------------------------------------
    #  Covariance Generation by Data-Data Distance
    for i in range(nobs):
        for j in range(i, nobs) :
            Cd[i][j] = np.linalg.norm(pos[i]-pos[j])
    #------------------------------------------------


    #------------------------------------------------
    # Variogram: Spherical Method
    for i in range(nobs) :
        for j in range(i, nobs) :
            if  Cd[i][j] < rnge :
                A[i][j] = A[j][i] = nget + sill*(1.5*Cd[i][j]/rnge - 0.5*(Cd[i][j]/rnge)**3)
            else:
                A[i][j] = A[j][i] = nget + sill
    #------------------------------------------------


    #---------initialize values--------
    posidim = len(pos[0])
    mesh = len(xx)

    cnt_x = (1. - 0.)/mesh
    cnt_y = (1. - 0.)/mesh

    vvval = np.ones((int(mesh),int(mesh)))


    #--------- estimate all location --------
    cord  = np.ones((posidim))

    for i in range(mesh):
        cord[0] = cnt_x*i+0.
        for j in range(mesh):
            cord[1] = cnt_y*j+0.
            cord[0] = xx[i,j]
            cord[1] = yy[i,j]

            #---Current to Obs Distance Yo ------------------
            for k in range(nobs) :

                distance = np.linalg.norm(cord-pos[k])

                if  distance < rnge :
                    b[k] = nget + sill*(1.5*distance/rnge - 0.5*(distance/rnge)**3)
                else:
                    b[k] = nget + sill
            #-------------------------------

            Weit  = linalg.solve(A,b)

            OKest = np.sum([Weit[i]*Obsp[i] for i in range(0, nobs-1)])

            vvval[i,j] = OKest

    #--------- Return! ---------
    return vvval



#-------------------------------------------------------------------
# Function for polynomial 2D

def polyfit2d(x, y, z, order):
    ncols = (order + 1)**2
    G = np.zeros((x.size, ncols))
    ij = itertools.product(range(order+1), range(order+1))
    for k, (i,j) in enumerate(ij):
        G[:,k] = x**i * y**j
    m, _, _, _ = np.linalg.lstsq(G, z)
    return m

#-------------------------------------------------------------------
# Function for polynomial 2D

def polyval2d(x, y, m):
    order = int(np.sqrt(len(m))) - 1
    ij = itertools.product(range(order+1), range(order+1))
    z = np.zeros_like(x)
    for a, (i,j) in zip(m, ij):
        z += a * x**i * y**j
    return z


#-------------------------------------------------------------------
# Function main
#-------------------------------------------------------------------


if __name__ == '__main__':
    main()


    from numpy import matrix
    from numpy import linalg

    from scipy.interpolate import Rbf


    #------------------------------------------
    # Get polynomial Coefficient : 2D, Random
    numdata = 50
    
    np.random.seed(65537)
    x = np.random.random(numdata) 
    y = np.random.random(numdata) 
  
    xy = np.ones((numdata,2))
    xy[:,0] = x/np.max(x)
    xy[:,1] = y/np.max(y)

    z  = x**2 + y**2 + 3*x**3 + y + np.random.random(numdata)*4 # Noise

    #------------------------------------------
    # Get polynomial Coefficient : 2D, Random
    mesh   = 50
    xx, yy = np.meshgrid(np.linspace(x.min(), x.max(), mesh), np.linspace(y.min(), y.max(), mesh))


    #------------------------------------------
    # Ordinary Kriging Estimation
    #------------------------------------------

    zz = Test_Okriging(x,y,z,xx,yy,0.0,1.0,0.35)

    fig = plt.figure()
    ax  = fig.add_subplot(121, projection='3d')
    ax.scatter(x, y, z)
    ax.plot_surface(xx, yy, zz,rstride = 1, cstride = 1, alpha=0.35, cmap=cm.jet)
    plt.title("Ordinary Kriging"); 
    ax.set_zlim3d(-z.min()-1, z.max()+1)

    #------------------------------------------
    # Polynomial fitting
    #------------------------------------------

    m = polyfit2d(x,y,z,3)      # Fit 2d polynomial
    zz = polyval2d(xx, yy, m)   # Meshing by polynomial

    #fig = plt.figure()
    ax = fig.add_subplot(122, projection='3d')
    ax.scatter(x, y, z)
    ax.plot_surface(xx, yy, zz, rstride=1, cstride=1, alpha=0.35, cmap=cm.jet)
    plt.title("Polynomial Regression"); 
    ax.set_zlim3d(-z.min()-1, z.max()+1)
    plt.show()